Example question: solve $2^n - 1 > 5n^2 - 4n$ , given that $n \in \mathbb{Z}^+$ (i.e. $n$ is a positive integer/whole number).

In our course of study we sometimes work with integer-valued variables (vs the usual real-numbered variables). For example, $n$ could be the number of terms in an AP/GP, or the number of trials in a binomial random variable. In addition to the methods discussed in the previous examples, there is a new method involving the GC table we can use when working with whole numbers.

Of course, we could use the graphical technique illustrated in example 1.4 . Doing so (when we use the GC for this question, we may have to adjust the graph window manually or use one of the zoom functions) will give us the solution $n > 8.279$. However, since $n$ is an integer, such a solution can be improved. We will round up 8.279 (understand why we round up rather than round down for this example?) and report our answer as $n \geq 9, n \in \mathbb{Z}$ .

The table method

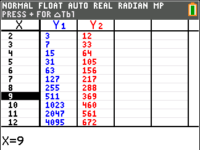
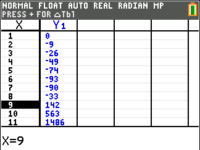
For integer-valued variables, it is often more convenient to use tables rather than graphs. We will key the expressions into the graphing calculator in the same manner we do for graphs. However, instead of pressing the "graph" button after that, we key the "table" button on top of it (the "2nd function" button followed by "graph"). This brings us to a table where the calculator has substituted different values into our expressions. Similar to the two methods in example 1.4 , we could either key two expressions, $2^n - 1$ and $5n^2-4n$ separately, or just one, $2^n - 1 - (5n^2-4n)$.

For the first approach, when we scroll through the values, we observe that $2^n-1$ (the blue "Y_1" in the second image) is less than or equal to $5x^2-4x$ (the red "Y_2" in the second image) for $n$ between 1 to 8. From 9 onwards, however, $2^n - 1$ is larger. This is what the question wants, giving us the solution $n \geq 9, n \in \mathbb{Z}$ .

For the second approach, we have rearranged the inequality to get $2^n-1-(5n^2-4n) > 0$. We thus scroll to look for when the expression is positive, arriving at the same answer as above.