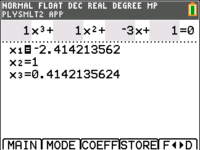
Example question: solve $x^3 + x^2 - 3x + 1 =0$.
In the "O" level Additional Math syllabus, we learned how to solve polynomials like $x^3 + x^2 - 3x + 1 =0$ using the factor theorem . We let $f(x) = x^3+x^2-3x+1$. By trial and error, we find that $f(1) = 0$ so $x=1$ is an answer and $x-1$ is a factor of $f(x)$. Long division (or comparing coefficients) gives us $f(x)=(x-1)(x^2+2x-1)$ and the quadratic formula gives us the other answers $-2.414, 0.414$. This method works, and is the recommended approach if we want exact solutions but can be really tedious to carry out. Moreover, there is no guarantee that a polynomial will have a "nice" answer like $x=1$, and even so we need a lucky bit of trial and error to proceed.
In example 1.4 we saw that we can use graphs in our GC to get the solutions. That is a much faster approach: sketch the graph and use the "zero" solver three times to get the solution.
The "zero" solver needs to be used up to $n$ times for a polynomial of degree $n$. (In the complex numbers topic, we will encounter the fundamental theorem of algebra which states that a polynomial of degree $n$ has, counted with multiplicity, exactly $n$ complex roots.) This can be potential tedious, in addition to having to set the graph window correctly to see all the roots. Thankfully, the GC has an app that makes solving this equation even faster.
To solve the question fast, press the "apps" button on your GC and choose the "PlySmlt2" application. Option 1 gives us the "Polynomial Root Finder". Set the appropriate settings (the order refers to the highest power of $x$ in our polynomial), key in the equation and press "Solve" to get all the answers at one go.