Example question: $\displaystyle y=\frac{x-1}{x^2+1}.$ Find, algebraically, the set of values that $y$ can take.
Other ways the question can be phrased:
1) Find, in exact form, the set of values $y$ can take.
2) Without using a calculator, find the set of values that $y$ can take.
3) Given $f(x) =\displaystyle \frac{x-1}{x^2+1} $ for $x \in \mathbb{R}$, use an algebraic method to determine the range of $f$.
$ \displaystyle y = \frac{x-1}{x^2+1} \\ y (x^2 + 1) = x-1 \\ yx^2 + y - x + 1 = 0 \\ yx^2 - x + (y+1) = 0 $
For the set of values $y$ can take, discriminant $b^2 -4ac \geq 0$.
$(-1)^2 - 4 y (y+1) \geq 0 \\ -4y^2 - 4y + 1 \geq 0 \\ 4y^2 + 4y - 1 \leq 0$.
Roots to $4y^2 + 4y - 1 = 0: \frac{-4 \pm \sqrt{4^2 - 4(4)(-1)}}{2(4)} = \frac{-4 \pm 4 \sqrt{2}}{8} = \frac{-1\pm \sqrt{2}}{2}$.
$ \frac{-1-\sqrt{2}}{2} \leq y \leq \frac{-1+\sqrt{2}}{2}$.
Set of values $y$ can take: $\left \{ y \in \mathbb{R}: \displaystyle \frac{-1-\sqrt{2}}{2} \leq y \leq \frac{-1+\sqrt{2}}{2} \right \}$.
Another accepted presentation of the solution: $\left [ \displaystyle \frac{-1-\sqrt{2}}{2}, \displaystyle -\frac{-1+\sqrt{2}}{2} \right ]$.
If this is the first time we have seen such a question, it may not be too clear what the question requires from us. To better understand the question, let us solve it using a graphical method.
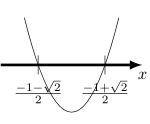
Sketching the graph of $\displaystyle y = \frac{x-1}{x^2+1}$ gives us the following.
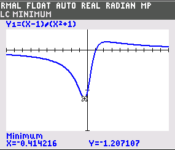
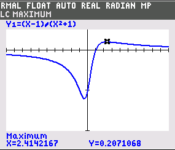
Observe that the $y$-coordinates of the curve cannot take all possible values. For example, the curve doesn't extend to $y=2$ and above. The question requires the range of values $y$ can take. For this curve, that will be between the maximum and minimum of the curve. Using the "minimum" and "maximum" solvers in our graphing calculator gives us the the coordinates of the stationary points, leading us to answer $-1.207 \leq y \leq 0.207 $.
We have an answer, but it is not in exact form. Differentiation (which is tedious) can give us that, but even then it doesn't satisfy the question's requirement of an algebraic method.
The main purpose to this section is to better understand the question. Now let us turn our attention to the algebraic approach.
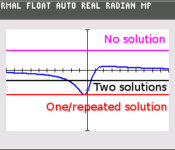
Let us go back to the graphs. Notice that for the values $y$ cannot take, if we were to draw a horizontal line across our graph it will not intersect the curve. Meanwhile, for the values $y$ can take, a horizontal line across our graph will cut the curve either once or twice. Recall we have a technique to distinguish the number of roots a quadratic equation has: the discriminant! We will use this concept in our solution.
Before we can apply the discriminant, we need to have a quadratic expression. As typical when working with fractions, we cross multiply and then move all terms to one side of the equation. The explains the first 3 lines of the solution above.
At this moment, the equation can look rather complicated as it contains two unknowns: $x$ and $y$. The trick is to treat the expression as one with just $x$ as the variable. We thus group all the $x^2$, $x$ and "constant" terms separately, leaving the "coefficients" in terms of $y$.
Since we want the set of values $y$ can take, we want one or two solutions to our equation. Thus the discriminant $b^2-4ac \geq 0$. We then solve the resulting quadratic inequality.
Our answer to the inequality is $ \frac{-1-\sqrt{2}}{2} \leq y \leq \frac{-1+\sqrt{2}}{2}$. Since the question requires a set of values, we express our answer as a set. Either the set-builder notation (the first boxed up answer) or the interval notation (the alternative presentation) above will be accepted.