Computing the result of vector addition is relatively intuitive:
$$ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{pmatrix}$$
For example, $ \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 1 \end{pmatrix}$

What is important is knowing when to use it and how to visualize the results. Recall that we use a "directed line segment" (an "arrow") to visualize a vector.

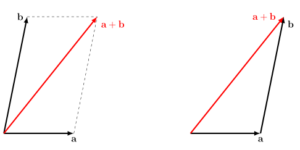
There are two ways to visualize $\mathbf{a} + \mathbf{b}$, as seen in the diagram below.

The first, on the left, is the "parallelogram law". Draw $\mathbf{a}$ and $\mathbf{b}$ starting from the same point. Construct a parallelogram using these two vectors, and the diagonal gives us the result $\mathbf{a}+\mathbf{b}$.

The alternative method, on the right, is to draw $\mathbf{a}$ and $\mathbf{b}$ "head-to-tail". Thereafter, we join the tail of the first vector to the head of the second, forming a triangle to visualize $\mathbf{a}+\mathbf{b}$.

The "parallelogram law" explains the solution to the example question: if $\overrightarrow{OA} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$, $ \overrightarrow{OB}= \begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix}$ and $OACB$ forms a parallelogram, then $\overrightarrow{OC}= \overrightarrow{OA} + \overrightarrow{OB} = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}$.

More practice

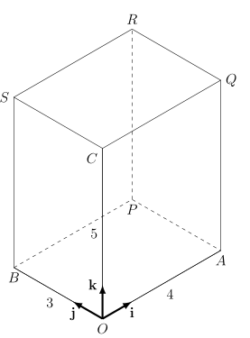
The diagram below shows a cuboid with base $OAPB$. $OA, OB$ and $OC$ are parallel to the $x$-, $y$- and $z$- axis respetively with magnitude $4,3$ and $5$ respectively.

Write down the following as column vectors: $\overrightarrow{OP}, \overrightarrow{OR}, \overrightarrow{QB}, \overrightarrow{RA}$.