Magnitude of a vector
The following gives us a formula to calculate the magnitude ("length") of a vector:
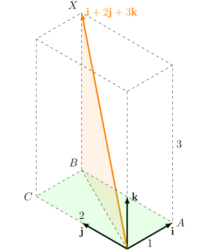
Consider, for example, the vector $\overrightarrow{OX} = \mathbf{i} + 2 \mathbf{j} + 3 \mathbf{k}$, as seen in the diagram below.
We wish to calculate the length of the line segment $OX$. We first apply Pythagoras Theorem on triangle $OAB$ to get $OB^2 = 1^2 + 2^2$. We then apply Pythagoras Theorem one more time on triangle $OBX$ to get $OX^2 = OB^2 + BX^2 = 1^2 + 2^2 + 3^2$. This gives us $OX = \sqrt{1^2+2^2+3^2}$.
Generalizing this example gives us
If you are interested in why we use the modulus $| \cdot |$ symbol for vector magnitude even though it behaves slightly different from the usual modulus/absolute values for real values (e.g. $|-2| = 2$), see this post.
Unit vectors
It is often useful to work with vectors of magnitude 1. We call such vectors unit vectors . Given any non-zero vector $\mathbf{a}$, we can scale it to produce a unit vector that is parallel to it. We denote this unit vector with the symbol $\hat{\mathbf{a}}$. The formula for $\hat{\mathbf{a}}$ is given by
One very useful application of unit vectors is given below and illustrated in example 2 below. See if you can understand the formula. Example 2 provides further explanation of why it works.
Solution to examples:
Answer: $|\mathbf{a}| = \sqrt{1^2 + (-1)^2 + 2^2} = \sqrt{6}$.
$\displaystyle \hat{\mathbf{a}} = \frac{1}{\sqrt{6}} (\mathbf{i} - \mathbf{j} + 2\mathbf{k})$.
A common first attempt is to think that $5 \mathbf{a}$ is our required answer. Unfortunately, that does not quite work. From example 1, we know that $|\mathbf{a}|=\sqrt{6}$ so $5\mathbf{a}$ will be of magnitude $5 \sqrt{6}$.
Instead, we first obtain a unit vector parallel to $\mathbf{a}$, $\hat{\mathbf{a}}$. Since it is a unit vector (of magnitude 1), $5 \hat{\mathbf{a}}$ gives us the required vector of magnitude 5 that is parallel to $\mathbf{a}$.
Answer: $\frac{5}{\sqrt{6}} (\mathbf{i}-\mathbf{j}+2\mathbf{k})$.