Position vectors
A vector comprises of magnitude and direction: the starting or ending position of the vector is not important. For example, the vector $\mathbf{a} = \mathbf{i} + 2 \mathbf{j}$ involves a movement of 1 unit along the $x$-axis and 2 units along the $y$-axis. It doesn't matter where it starts from: any such movement are all considered $\mathbf{a}$. In fact, vectors can be "moved around" as long as we keep it parallel and maintain its magnitude.
When we study geometry (in particular, 3-dimensional geometry for our syllabus) it is often useful to work with points. We have already worked with coordinates in curve sketching and can write, for example, the coordinates of a point $A$ to be $(1,2,0)$. We let the origin $O$ be $(0,0,0)$ and thus have a vector $\overrightarrow{OA} = \mathbf{i}+2\mathbf{j}$.
However, we will "lose track" of the point $A$ if we allow the vector $\overrightarrow{OA}$ to "move". To handle this discrepancy, we call the vectors that originate from the origin and end at a point the position vector of the point. This special vector is often handled slightly differently from a general (direction) vector. A position vector is generally considered to be "fixed" while direction vectors can be "moved around".
Notationally for our syllabus, we write coordinates horizontally, for example, $B (1,-3,2)$ and represent position vectors in column vector form ($\overrightarrow{OB}=\mathbf{b}=\begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}$). Using $\mathbf{i},\mathbf{j}$ and $\mathbf{k}$ will work for the latter as well.
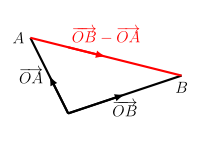
We are often interested to form a vector starting from a point $A$ and ending at a point $B$. Using concepts from vector addtion and subtraction, we get $\overrightarrow{AB}=\overrightarrow{AO} + \overrightarrow{OB} = \overrightarrow{OB}-\overrightarrow{OA}$. This is illustated in the diagram below.
This seemingly trivial formula is especially useful and will be used very often in our syllabus since it allows us to go from coordinates/position vectors to a vector starting from one point and ending at another.
Distance between points
We now know how to calculate $\overrightarrow{AB}$. To find the the distance between two points, $A$ and $B$, we use the magnitude of $\overrightarrow{AB}$, $\left | \overrightarrow{AB} \right |$.
Collinear points
We are sometimes interested in whether three points lie on a straight line. If they do, we call them collinear . To check whether 3 points $A,B$ and $C$ are collinear, we can form the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$ (other combinations like $\overrightarrow{BC}$ and $\overrightarrow{CB}$ are allowed too). If $A,B$ and $C$ are collinear, then $\overrightarrow{AB}$ and $\overrightarrow{AC}$ will be parallel so $\overrightarrow{AB}=k\overrightarrow{AC}$.
Conversely, if $\overrightarrow{AB}=k\overrightarrow{AC}$ for some $k \neq 0$, then $\overrightarrow{AB}$ and $\overrightarrow{AC}$ are parallel. Moreover, they share a common point $A$ so $A,B$ and $C$ must collinear.
Solutions to examples
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} =$ $-4 \mathbf{i} + 3 \mathbf{j} -7\mathbf{k}$.
Distance required $=|\overrightarrow{AB}| =$ $\sqrt{74}$ units.
$\overrightarrow{AC} = \overrightarrow{OC}-\overrightarrow{OA} =
\begin{pmatrix} 8 \\ y+1 \\ 14 \end{pmatrix}$.
Since $A,B$ and $C$ are collinear, $\overrightarrow{AC} = k \overrightarrow{AB}$ for some $k$.
$\begin{pmatrix} 8 \\ y+1 \\ 14 \end{pmatrix} = k\begin{pmatrix} -4 \\ 3 \\ -7 \end{pmatrix}$.
Hence $k = -2$ and $y+1 = (-2)(-4)$. This gives $y=7$.
$\overrightarrow{AD} = \overrightarrow{OD} - \overrightarrow{OA} = -8\mathbf{i} + 6 \mathbf{j} -14 \mathbf{k}$.
Hence $\overrightarrow{AD} = 2 \overrightarrow{AB}$, so $AD$ is parallel to $AB$.
Moreover, they share a common point $A$.
Thus $A,B$ and $D$ lie on the same line.