By product rule, $\displaystyle \frac{\mathrm{d}(uv)}{\mathrm{d}x} = u \frac{\mathrm{d}v}{\mathrm{d}x} + \frac{\mathrm{d}u}{\mathrm{d}x} v$.

Rearranging it gives us $\displaystyle u \frac{\mathrm{d}v}{\mathrm{d}x} = \frac{\mathrm{d}(uv)}{\mathrm{d}x} -\frac{\mathrm{d}u}{\mathrm{d}x} v$.

Integrating, we get $\displaystyle \int u \frac{\mathrm{d}v}{\mathrm{d}x} \; \mathrm{d}x = \int \frac{\mathrm{d}(uv)}{\mathrm{d}x} -\frac{\mathrm{d}u}{\mathrm{d}x} v \mathrm{d}x$.

We split up the integral: $\displaystyle \int u \frac{\mathrm{d}v}{\mathrm{d}x} \; \mathrm{d}x = \int \frac{\mathrm{d}(uv)}{\mathrm{d}x} \; \mathrm{d}x - \int \frac{\mathrm{d}u}{\mathrm{d}x} v \mathrm{d}x$.

Since integration is the reverse of differentiation, $\displaystyle \int \frac{\mathrm{d}(uv)}{\mathrm{d}x} = uv$.
This gives us our integration by parts formula $\displaystyle \int u \frac{\mathrm{d}v}{\mathrm{d}x} \; \mathrm{d}x = uv - \int \frac{\mathrm{d}u}{\mathrm{d}x} v \mathrm{d}x$

So how do we use the integration by parts formula? We split up our integrand into two parts. One part, which we will denote $u$, will be differentiated to get $\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x}$. The remaining part, denoted by $\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$, is integrated it to get $v$.

Notice that unlike all the 3 integration techniques covered so far (the use of $f'(x)$, handling rational functions and using trigonometric identities), the integration by parts formula still gives us an integration sign on the right hand side: it means that our job is not done yet!

That has two implications for us. First, it means that, when given a fresh integration question, we should try whether any of the first 3 techniques work before considering using integration by parts. If the other techniques work, they give us a solution in a couple of steps. This is much better than applying the rather cumbersome integration by parts formula.

Second, it means that for integration by parts to work, we need to be able to integrate $\displaystyle \int \frac{\mathrm{d}u}{\mathrm{d}x} v \; \mathrm{d}x$. It should be simpler than what we started off with. A heuristic to help achieve this will be given in the next section.

For now, let us observe the formula in action for the first example. We let $u$ be $x$ and $\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$ be $\mathrm{e}^{3x}$. (How to make the choice? Read the next section!) Hence $\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x} = 1$ and $\displaystyle v= \frac{\mathrm{e}^{3x}}{3}$.
We apply the by parts formula to get $\displaystyle \int x \mathrm{e}^{3x} \; \mathrm{d}x = x \frac{\mathrm{e}^{3x}}{3} - \int \frac{\mathrm{e}^{3x}}{3} \; \mathrm{d}x $. Thankfully $\displaystyle \frac{\mathrm{e}^{3x}}{3}$ can be integrated so we proceed with one more integration step to get the answer $\displaystyle \frac{x \, \mathrm{e}^{3x}}{3} - \frac{\mathrm{e}^{3x}}{9} + C$.

To emphasize, for the by parts formula to work, the new integrand $\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x} v$ should be simpler than the original. We may sometimes apply the formula more than once (sometimes twice, sometimes even $n$ times) before we get our answer. If our working gets more complicated with the application of the formula, we may be on the wrong track. Perhaps we have to switch our "$u$"s and "$\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$"s around; perhaps we have to split up our integrand a different way; or perhaps the question shouldn't even be tackled with the by parts formula.

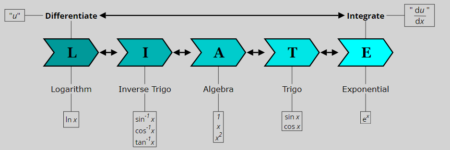
The acronym/initialism "LIATE" is a useful heuristic to divide how to assign each "part" in our by parts formula. Each letter correspond to a common class of function in our study: "L" for logarithms (usually $\ln x$), "I" for the inverse trigonometric functions (usually $\sin^{-1} x, \cos^{-1} x$ and $\tan^{-1}$, "A" for algebra, which may refer to constants like $1$ or $2$, or polynomials like $x$ and $x^2$. "T" refers to the trigonometric functions (usually $\sin x$ and $\cos x$) while "E" represents the exponential function (usually $\mathrm{e}^x$.

We will think of them broadly as 3 groups. The first, "LI" , consists of functions we do not know how to integrate. However, we do know that the differentiation of $\ln x$ is $\frac{1}{x}$ while the differentiations of the inverse trigonometric functions are provided in the formula list MF26.
$\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \left ( \sin^{-1} x \right ) = \frac{1}{\sqrt{1-x^2}} \\ \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \left ( \cos^{-1}x \right ) = \frac{-1}{\sqrt{1-x^2}} \\ \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \left ( \tan^{-1} x \right ) = \frac{1}{1+x^2}$
As such, when encountering these functions, it is often prudent to designate them as "$u$" and differentiate them.

On the other end of the spectrum we have the groupe "TE" consisting of the trigonometric and exponential functions. $\sin x, \cos x$ and $\mathrm{e}^x$ have similar characteristics it that they behave similarly under differentiation and integration. Differentiation is more powerful and is usually reserved for the other three "LIA" functions. Thus, we typically designate $\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$ for the "TE" functions and integrate them.

In the middle we have the "A" group with terms like $1$, $x$ and $x^2$. These terms can be integrated or differentiated. Ideally, differentiation simplifies our expressions (for example, $x^2$ becomes $2x$) so when "A" is paired with "T/E", we let $u$ be our algebra term and differentiate it. In cases where an algebraic term is paired with "L/I" functions, however, priority for differentiation goes to those function so we let $\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$ be the algebraic term and integrate them.

This explain why, in the previous example, we let $u$ be $x$ and $\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}$ be $\mathrm{e}^{3x}$.

A word of warning, however: "LIATE" is just a heuristic. While useful, there will be times where it will fail. Certain tougher questions call for more "creative" ways to split up the parts so be nimble and flexible in the cases when applying the by parts formula fail to simplify our working.

If it is the first time we are encountering questions like $\displaystyle \int \ln x \; \mathrm{d}x$ , it may not be clear to use the by parts formula at all. After all, to apply the formula we split the integrand up into two parts, one to differentiate and one to integrate. For this example, there is only one term $\ln x$. So where are the parts?

It turns out, the other part is hidden: it is the constant $1$ (since $1 \cdot \ln x = \ln x$). Try to follow the heuristic described in the previous section and decide whether we designate $1$ or $\ln x$ to be integrated or differentiated. If we have made the correct choice, the following worked solution should make sense.

$\displaystyle \int \ln x \; \mathrm{d}x \\ = \displaystyle x \ln x - \int x \frac{1}{x} \; \mathrm{d}x \\ = \displaystyle x \ln x - \int 1 \; \mathrm{d}x$
$=$ $x \ln x - x + C.$