Example 1

$\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x} = 2 \\ \displaystyle \int x \sqrt{2x-3} \; \mathrm{d}x \\ = \displaystyle \int \frac{u+3}{2} \sqrt{u} \, \left ( \frac{1}{2} \right ) \; \mathrm{d}u \\ = \displaystyle \frac{1}{4} \int u^{\frac{3}{2}} + 3 u^{\frac{1}{2}} \; \mathrm{d}u \\ = \displaystyle \frac{1}{4} \left ( \frac{u^{\frac{5}{2}}}{\frac{5}{2}} + \frac{3u^{\frac{3}{2}}}{\frac{3}{2}} \right ) + C \\ = \displaystyle \frac{u^{\frac{5}{2}}}{10} + \frac{ u^{\frac{3}{2}}}{2} + C$
$=$ $\displaystyle \frac{(2x-3)^{\frac{5}{2}}}{10} + \frac{ (2x-3)^{\frac{3}{2}} }{2} + C$

Example 2

$\displaystyle \frac{\mathrm{d}x}{\mathrm{d}\theta} = \cos \theta \\ \displaystyle \int \sqrt{1-x^2} \; \mathrm{d}x \\ = \displaystyle \int \sqrt{1-\sin^2 \theta} \, \cos \theta \; \mathrm{d} \theta \\ = \displaystyle \int \sqrt{\cos^2 \theta} \, \cos \theta \; \mathrm{d} \theta \\ = \displaystyle \int \cos^2 \theta \; \mathrm{d} \theta \\ = \displaystyle \int \frac{\cos 2 \theta + 1}{2} \; \mathrm{d} \theta \\ = \displaystyle \frac{\sin 2 \theta}{4} + \frac{\theta}{2} + C \\ = \displaystyle \frac{2 \sin \theta \cos \theta}{4} + \frac{\theta}{2} + C$
$=$ $\displaystyle \frac{x \sqrt{1-x^2}}{2} + \frac{\sin^{-1} x}{2} + C$

The aim of integration by substitution is to transform our integral from one in which we do not know how to do to one that we do. This is accomplished by changing our variable ($x$ in our examples) to a different one ($u, \theta$ for our examples). By chain rule $\int \cdot \; \mathrm{d}x = \int \cdot \frac{\mathrm{d}x}{\mathrm{d}u} \mathrm{d}u$. Hence we start off integration by substitution by differentiating the given substitution to facilitate our next step in applying that formula.

A very common mistake is to simply replace $\mathrm{d}x$ with $\mathrm{d}\theta$. Remember not to do that. One way to accomplish this is to always start with differentiation .

We are now ready to tackle the integral. Our next aim is to perform substitution: substitute away all "$x$"s to the new variable, and replace $\mathrm{d}x$ with $\frac{\mathrm{d}x}{\mathrm{d}u} \mathrm{d}u$ (where $u$ stands for the new variable that is being introduced)$.

For example 1, we replace the $2x-3$ we see in the square root with $u$. Algebraic manipulation gives us $x = \frac{u+3}{2}$ so we replace $x$ with that. From step 1, $\frac{\mathrm{d}x}{\mathrm{d}u} = \frac{1}{2}$ so replace $\mathrm{d}x$ with $\frac{1}{2} \mathrm{d}u$.

A similar approach is carried out for example 2.

Assuming an appropriate substitution was given and we have carried out steps 1 and 2 correctly, the new integral in terms of the new variable should be one we are able to integrate. Typically this will be an integral of the types seen from example 8.0 all the way to example 8.3. (We can review them starting from this page.

For example 1 in this section, we perform some algebraic manipulation (with indices) to get $\displaystyle \frac{u^{\frac{3}{2}}+3u^{\frac{3}{2}}}{4}$. The two terms are easily integrated with our basic integral formulas.

For example 2, we apply the Pythagorean identity to simplify our expression and proceed until we arrive at $\cos^2 \theta$. We have seen such an integral in example 8.3a . We thus apply the double angle formula and proceed with integration.

A common mistake is to end at step 3. After all, we have finished integration, which was the point of the question. However, we are not done yet because the question was given in the original variable ($x$ for our examples), while our answers are in the new variables ($u, \theta$) in step 3. We must thus remember to substitute back .

This can be done reasonably simply in example 1. $u = 2x-3$ so we just plug that in and we are done.

For example 2, $x = \sin \theta$ so $\theta = \sin^{-1} x$. This can be used to replace $\frac{\theta}{2}$ with $\frac{\sin^{-1}x}{2}$ but gives rise to an unwieldy expression $\frac{\sin (2 \sin^{-1} x)}{4}$ if we substitute into $\frac{\sin 2 \theta}{4}$. Such expressions should be simplified. To simplify it, let us not substitute $\theta$ into the trigonometric function yet. We first observe that $\sin 2 \theta$ has an argument $2 \theta$ while our original substitution is $x = \sin \theta$ with argument $\theta$. We thus apply the double angle formula $\sin 2 \theta = 2 \sin \theta \cos \theta$. $\sin \theta$ can now be replaced with $x$.

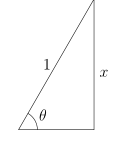
What about $\cos \theta$? There are two (equivalent) approaches: one is to use the Pythagorean identities. The other, which I prefer, is to construct a right angle triangle. $\sin \theta = x = \frac{x}{1}$ so we label the triangle with an angle $\theta$, opposite side $x$ and hypotenuse $1$.

By Pythagoras Theorem the remaining side is $\sqrt{1-x^2}$. This right angle triangle thus allow us to visualize all trigonometric ratios. In particular, $\cos \theta = \frac{\sqrt{1-x^2}}{1} = \sqrt{1-x^2}$. Substitute this and we will have arrived at a simplified answer in terms of the original variable $x$.