11b.2. The cross product, normal vectors, areas

The cross product

The cross product (sometimes also called the vector product ) is defined as follows: $$ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \times \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_2 b_3 - b_2 a_3 \\ -(a_1 b_3 - b_1 a_3) \\ a_1 b_2 - b_1 a_2 \end{pmatrix} $$ It is a bit unwieldy: we should practice the computation until we can reproduce it accurately.

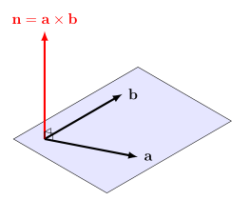
Normal vectors and areas

There are 2 main reasons for introducing the cross product. The first is that the result of the cross product, $\mathbf{n} = \mathbf{a} \times \mathbf{b}$ is a vector that is perpendicular to both $\mathbf{a}$ and $\mathbf{b}$. This is sometimes called the normal vector and will be used extensively in chapter 11c when we work with planes in 3 dimensions.

The second is that the cross product leads to a formula very similar to the dot product formula we encountered in the previous section:

$ | \mathbf{a} \times \mathbf{b} | = |\mathbf{a}| \, |\mathbf{b}| \sin \theta$

where $\theta$ is the angle between vectors $\mathbf{a}$ and $\mathbf{b}$. Notice the two differences between this and the dot product formula: first we take the magnitude of $\mathbf{a} \times \mathbf{b}$ on the LHS of the equation, and second we have a sine instead of a cosine.

The derivation of the formula is a bit out of our scope so we will take the formula as is. Hopefully the formula doesn't sound too foreign to us: we have seen it in the calculation of areas of triangles and parallelograms in previous study. This gives us two formulas:

$\textrm{Area of triangle formed by } \mathbf{a} \textrm{ and } \mathbf{b}$: $\frac{1}{2} | \mathbf{a} \times \mathbf{b} |$
$\textrm{Area of parallelogram formed by } \mathbf{a} \textrm{ and } \mathbf{b}$: $| \mathbf{a} \times \mathbf{b} |$

Solution to examples

1. Points $A$ and $B$ have coordinates $A(1,2,-3)$ and $B(5,0,1)$.
Find a vector $\mathbf{n}$, such that $\mathbf{n}$ is perpendicular to $\overrightarrow{OA}$ and $\overrightarrow{OB}$.

Solution: $\mathbf{n} = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} \times \begin{pmatrix} 5 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ -16 \\ -10 \end{pmatrix}$
Remark: Any parallel vector will work as an answer.

2. Find the area of triangle $OAB$.

Solution: Area of triangle $OAB = \frac{1}{2} | \mathbf{a} \times \mathbf{b} | = \frac{1}{2} | 2\mathbf{i} - 16 \mathbf{j} - 10 \mathbf{k}| =$ $3\sqrt{10}$ $\mathrm{units}^2$.